ソフトウェアのテストは、ソフトウェアの品質を高める上で非常に重要な工程です。限られた予算やスケジュールの中、テストで効率よく不具合を発見するためには適切なテストケースを作成することが欠かせません。失敗しないテストケースを作るためには、テスト技法に関する理解を深めることが大事になりますが、今回はブラックボックステストにおいてよく使われる同値分割法についてご紹介します。

なお、ブラックボックステストについてお知りになりたい方は、以下の記事をご参照ください。
ソフトウェアテスト技法のひとつ、ブラックボックステストとは｜その特徴や技法について

また、テスト技法全般についてお知りになりたい方は、以下の記事をご参照ください。
ソフトウェアテスト技法とは | 主な技法の種類や特徴について解説

1. 同値分割法とは？

同値分割法は、システム上で同等に処理される（＝出力結果が同じになる）と想定されるデータを「同値パーティション」または「同値クラス」と呼ばれるグループに振り分け、そのなかの代表的なデータを用いてテストを行う技法です。
ここでは、呼び方を「同値クラス」で統一します。

この技法は、仕様に基づいた包括的なブラックボックステスト技法のひとつであり、少ないテスト回数でより広い範囲をカバーできるという特徴があります。
また、同値分割法はあらゆるレベルのテストにも適用することが可能です。

同値分割法の背後にある理論では、同値クラス中から1つの条件/値のテスト結果が「合格」であれば、同値クラス内の他のすべての条件/値もまた「合格」となるという考え方を採用しています。同様に、同値クラス中から1つの条件/値のテスト結果が「不合格」であれば、同値クラス内の他のすべての条件/値も「不合格」とみなされます。
わかりやすくするために、簡単な例を挙げてご説明します。

例えば、「1から3までの整数」を入力したときの出力が「A」、「4から6までの整数」を入力したときの出力が「B」となるシステムをテストするとします。
このとき、1から3までの整数（つまり1、2、3）と、4から6までの整数（つまり4、5、6）はそれぞれ同値クラスとなります。

同値分割法を用いたテストの仕方としては、例えば「2」を入力して「A」が出力された場合、同値クラスに含まれる1と3はテストをせずとも「1から3までの整数」を入力したときに「A」が正しく出力されるとみなします。
同様に、例えば「6」を入力して「B」と出力されなかった場合、同値クラスに含まれる4と5はテストをすることなく「4から6までの整数」を入力したときに「B」が正しく出力されない（つまり不具合）とみなします。

このように、同値クラスに存在するすべての条件/値を対象とする代わりに、各同値クラスに含まれる任意の値だけをテストすればよく、その分、効率良くテストを進めることが可能というのが同値分割法の最も大きなメリットとなります。

ただし、上の例の場合では「2」を入力した際に正しく「A」が出力されることは確認できたものの、「1」や「3」を入力した際に不具合が発生する可能性が残ります。
そのため、より不具合検出の精度を上げるために「境界値分析」というテスト技法もあわせて用いられることが一般的です。

適切なテストケース作成に役立つ技法を知る2： 境界値分析とは？

なお、同値クラスは各入力状態（通常は仕様内の文または句）を取得し、それを2つ以上のグループに分割することによって決定されます。
また、同値クラスには「有効な同値クラス」と「無効な同値クラス」の2種類が存在します。

2. 同値分割法の留意点

同値分割法を使用する場合に留意したい項目を以下にまとめました。

• 有効な同値クラスと無効な同値クラスを正しく識別する必要があります。
  • 有効な値は、コンポーネントまたはシステムによって受け入れられる値です。有効な値を含むグループは、「有効な同値クラス」と呼ばれます。
  • 無効な値は、コンポーネントまたはシステムによって拒否された値です。無効な値を含むグループは、「無効な同値クラス」と呼ばれます。
• 必要に応じて、任意の同値クラスをサブ同値クラスに分割できます。
• テストケースで無効な同値クラスを使用する場合、エラーがカバーされないことを保証するために、それらを個別にテストする必要があります。

つまり、他の無効な同値クラスと組み合わせたテストは避けるようにします。その理由は、複数の障害が同時に発生するとそのうちの1つだけが表示されて他の障害が検出されず、バグが隠されるリスクがあるためです。

3. 同値分割法によるテストケースの設計手順

次に、同値分割法を使ったテストケースを設計する手順として以下の3ステップを紹介します。

• ステップ1：システムが同等に扱われる条件/入力値をグループに分割して各同値クラスを定義します。
• ステップ2：各同値クラスを表すランダムな値を選択します。
• ステップ3：ステップ2で選択した値に従ってテストケースを設計します。

4. 同値分割の例題

例えば、以下の仕様に基づき、ピザ注文アプリで数量入力ボックスを検証するとしましょう。

まず上記の仕様をもとにした場合、次のようにテスト条件を決定できます。

• Pizza Orderテキストボックスに入力された数値のうち、10より大きい数字(11など)は無効と見なされる。
• 1未満(0以下)の数値は無効と見なされる。
• 1から10までの数字は有効と見なされる。

問題は、可能なすべての値をテストするとテストケースの数が非常に多くなってしまうことです。多くの開発現場では限られた人的リソースと時間の中でテスト工程を行う必要があるため、すべてのテストケースを網羅することは現実的ではありません。
この問題を解決するために、同値分割法を使用し、以下の図のように顧客が入力したピザの数値を異なるグループに分割します。

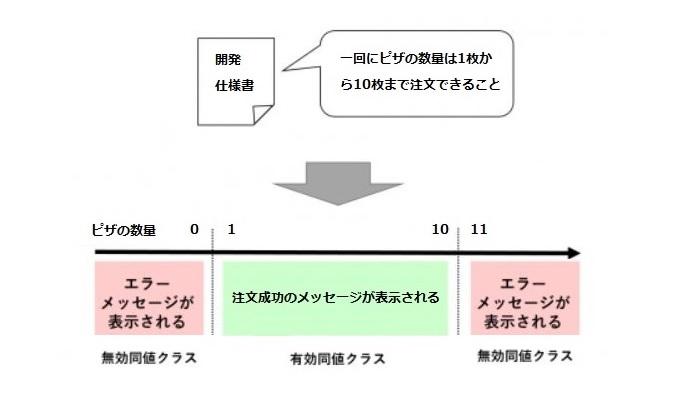
この作業では、以下の３つの同値クラスに分けることができます。

• x <1 (有効な同値クラス)
• 1 <=x <= 10 (有効な同値クラス)
• x > 10 (無効な同値クラス)

次のステップでは、各同値クラスからテスト用の値をランダムに選択します。下記の図では、3つの同値クラスを表す-6、5、115と3つの値を選択します。

最後に、下記のテストケースを作成することができます。

• ケース1：テキストボックスに「-6」を入力　⇒　エラーが表示される。
• ケース2：テキストボックスに「5」を入力　⇒　エラーは表示されず、注文成功のメッセージが表示される
• ケース3：テキストボックスに「115」を入力　⇒　エラーが表示される。

5. 同値分類法の利点と欠点

最後に、同値分割法のメリットやデメリットを以下にまとめました。

メリット
各同値クラスを代表的な要素でテストをするため、網羅性を担保しながらテストケースの数が大幅に削減されます。
その結果、テストの実行にかかる時間やコストも大幅に削減されます。

デメリット
すべてのシステムにこのテスト技法を適用できるわけではありません。
また、各同値クラスからランダムな値のみを選択しテストすることで、ある一定の障害を見逃す可能性があります。一部の研究では、同値クラスの境界値をテストするときにエラーの大半が見つかることが示されています。

同値分割法は少ないテスト回数でより広い範囲をカバーするために有効なテスト手法ではありますが、システムによっては障害を見逃す可能性もあります。このため、実際のテスト現場では境界値分析と呼ばれるテスト技法を併用しながら、テストを実施することが一般的です。

境界値分析については以下の記事で詳しくご紹介していますので、ぜひこちらも併せてご参照ください。
適切なテストケース作成に役立つ技法を知る2： 境界値分析とは？

SHIFT ASIAは品質保証とソフトウェア開発のプロフェッショナルとして、ベトナムを拠点にソフトウェアテスト事業・オフショア開発事業を展開しています。

SHIFT ASIAのソリューションや導入事例についてはトップメニューのタブメニューから詳細をご覧いただけますので、ソフトウェアのテストや開発に関して課題やお悩みなどがございましたら、いつでもお気軽にご相談いただけると幸いです。