適切なテストケース作成に役立つ技法を知る2：境界値分析とは？

前回の私の記事で紹介した同値分割法に続き、今回はブラックボックステストで同じく一般的によく使われる技法のひとつである「境界値分析」について解説します。

1.境界値分析とは？

境界値分析は、出力が同じ結果になるような入力値を同値クラスとしてグループにまとめた上で、グループが隣接する境界やその前後の値を入力としてテストを行う手法です。出力結果が変化する境界付近では不具合が多く発生しやすいという経験則に基づき、その付近の入力値を重点的に検証することで効率良く不具合を調べることができます。

境界値分析は，同値クラスの間の境界の値（境界値）をテストデータとして選択するため、同値分割法を拡張した技法とも言えます。境界値は各同値クラスの最小値と最大値、または最初と最後の値となり、数値または連続データで構成され、ソートされていることが条件となります。

2. .境界値分析によるテストケースの設計手順

境界値分析は境界値に対して2ポイント選ぶ場合と、3ポイント選ぶ場合がありますが、3ポイントの場合は境界の前後と境界の3つの値を使用します。それでは以下に具体的なテストケースの設計手順を説明していきます。

• ステップ１: システムが同等に扱われる条件/入力値をグループに分割して各同値クラスを定義します。

• ステップ2: ステップ１で各同値クラスの境界値を選定します。（通常、境界値は各同値クラスの最小値と最大値、または最初と最後の値になります）

• ステップ 3: ステップ 2 で選択した値に従ってテストケースを設計します。

3. .境界値分析の例題

例えば、以下の仕様に基づき、ピザ注文アプリで数量入力ボックスを検証する場合を考えてみましょう。

仕様:
• 1 から 10 まで入力されたピザの数量は有効と見なされる。その場合、注文成功メッセージが表示される。

• それ以外の値は注文に対して無効とみなされ、「注文ごとにピザの数量を1から10までご選択ください！」というエラーが表示される。

※システムが整数のみを受け入れると仮定します。

まず上記の仕様をもとに同値分割法の時と同じく、各同値クラスを決定します。この作業では、以下の３つの同値クラスに分けることができます。

• x <1 (有効な同値クラス)
• 1 <=x <= 10 (有効な同値クラス) • x > 10 (無効な同値クラス)

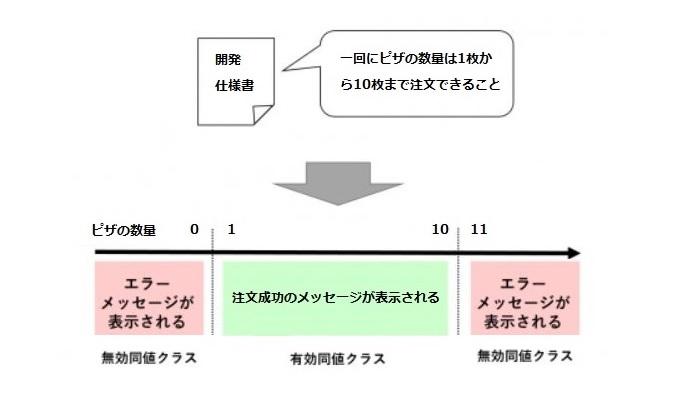
次に同値クラスを分割した後、テストのために各同値クラスでランダムな値を選択するのではなく、これらのクラスの境界値を選択します。

今回のケースでは以下の図版の赤丸で囲った数字がそれぞれの同値クラスの最小値、最大値となります。

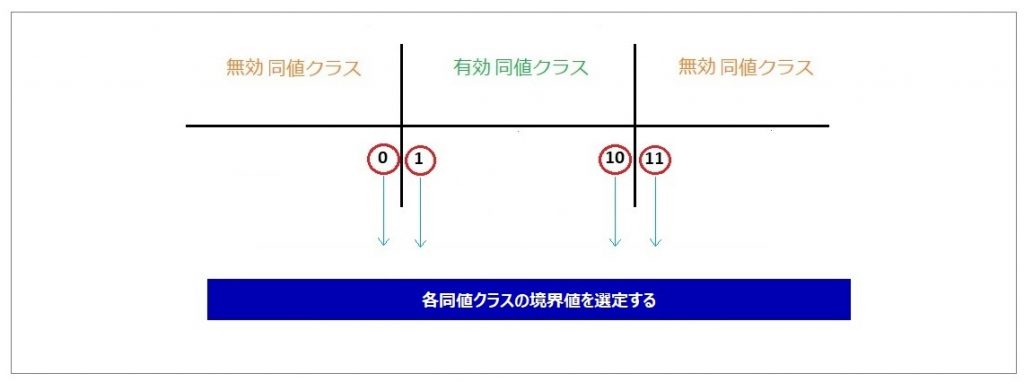
この結果、以下のテストケースを作成することができます。

•　Case 1: テキストボックスに「0」を入力 ⇒ エラーが表示
•　Case 2: テキストボックスに「1」を入力 ⇒ エラーは表示されず、注文成功のメッセージが表示
•　Case 3: テキストボックスに「10」を入力 ⇒ エラーは表示されず、注文成功のメッセージが表示
•　Case 4: テキストボックスに「11」を入力 ⇒ エラーが表示

4. 境界値分析の利点と欠点

最後に、境界値分析のメリットやデメリットを以下にまとめました。

利点
同値分割法と同様にテストケースの数を大幅に削減することで、テストケースの設計とテストの実行にかかる時間を節約することができます。さらに、同値クラスでランダムな値をテストするのではなく、エラーが隠されていることが多い同値クラスの境界値を中心に検証するため、同値分割法と比べても障害を発見できる可能性がより高くなります。

欠点
入力変数が互いに独立しているため、それぞれの引数の値の範囲が有限である場合にのみ有効な手法となります。

同値分割法や境界値分析は、ブラックボックステストを効率よく実行する上での基本となる技法なので、それぞれの利点や欠点も含め、しっかりと理解しておきましょう。

SHIFT ASIAは品質保証とソフトウェア開発のプロフェッショナルとして、ベトナムを拠点にソフトウェアテスト事業・オフショア開発事業を展開しています。

SHIFT ASIAのソリューションや導入事例についてはトップメニューのタブメニューから詳細をご覧いただけますので、何かございましたらいつでもお気軽にご相談いただけると幸いです。